An Algebraic and Geometric Approach to Eigenvalues and Eigenvectors

In linear algebra, we are introduced to eigenvectors and eigenvalues. While eigenvectors are vectors with a direction immutable by a transformation, eigenvalues are associated with the physical quantity by which the eigenvector is scaled. 

For the average student, most of these concepts can be difficult to grasp from a geometric perspective. That is why, in the following sections, I will utilize visual representations in addition to manipulating symbols algebraically. 

The fundamental formula that characterizes the eigenvectors and eigenvalues of a matrix is Av = λv. In which A is a matrix, v is an eigenvector, λ (lambda) is an eigenvalue, and v is an eigenvector.

Let’s begin by considering the given 2×2 matrix.

 [ 2, 3

      5, 4 ]

Where our eigenvectors are:

[ 3      and      [ -1

    5 ]                   1 ] 

With corresponding eigenvalues of λ1 = 7 and λ2 = -1.

To arrive at these conclusions, our first step consists of subtracting λ from the diagonal entries, much like this:

[ 2 – λ, 3

      5, 4 – λ  ]

Wherefore the characteristic equation, or determinant, of our matrix, is:

(λ – 7) (λ +1) = 0

We end up with λ1 = 7 and λ2 = -1 as our eigenvalues. Now, we will input the different values of λ into our previous equation.

[ 2 – 7, 3     =    [ -5, 3 

     5, 4 – 7  ]           5, -3 ]

And

[ 2 – -1, 3     =    [ 3, 3 

    5, 4 – -1  ]          5, 5 ]

Where the null spaces of our matrix, found by satisfying the equation Ax = 0, are:

λ1 = {[ 3

                5 ]}

And

λ2 = {[ -1

                 1 ]}

This is how we reach the aforementioned solutions. On another note, a visual that can accurately represent our conclusion would be the following:

Image source

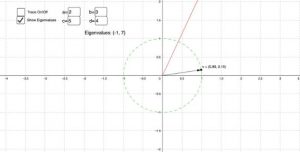
Hopefully, with this brief overview, you’ve been able to gain some confidence in your ability to calculate and visualize eigenvectors and eigenvalues from an algebraic and geometric point of view.

By: Estefania Olaiz

March 19, 2022

Sources:

1. https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors#:~:text=Geometrically%2C%20an%20eigenvector%2C%20corresponding%20to,negative%2C%20the%20direction%20is%20reversed.
2. https://www.mathsisfun.com/algebra/eigenvalue.html 
3. https://lpsa.swarthmore.edu/MtrxVibe/EigMat/MatrixEigen.html
4. https://www.mathsisfun.com/algebra/matrix-determinant.html 
5. https://www.geogebra.org/m/JP2XZpzV